|
การวิเคราะห์ข้อมูลทางสถิติ
|
 ♥ ♥ |
|
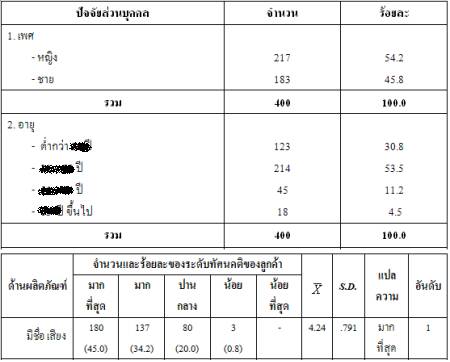
การวิเคราะห์ข้อมูลทางสถิติ
เครื่องมือสำหรับการวิเคราะห์ข้อมูลทางสถิติ คือ โปรแกรมสำหรับการวิเคราะห์ข้อมูลทางสถิติที่มีผลลัพธ์ในหลายรูปแบบ เช่น ตาราง หรือแผนภูมิ เป็นโปรแกรมสามารถที่เก็บบันทึกข้อมูล นำมาประมวลผล และแสดงผลลัพธ์ออกมาเป็นรายงานที่เข้าใจได้ง่าย สามารถเลือกใช้ค่าสถิติได้อย่างครบถ้วน เช่น การแจกแจงความถี่ การวัดค่ากลางของข้อมูล การวัดการกระจาย หรือการวัดลักษณะของเส้นโค้ง
|
อ่านเพิ่มเติม
Thaiall.com
 ♥
♥ ♥
♥